可视化数据分布

在任何分析或建模数据的努力中，第一步应该是了解变量是如何分布的。用于分布可视化的技术可以快速回答许多重要的问题。观测值覆盖的范围是什么？它们的中心趋势是什么？它们在一个方向上严重倾斜吗？是否有双峰性的证据？是否有明显的异常值？这些问题的答案是否因其他变量定义的子集而异？

分布模块包含几个旨在回答此类问题的函数。轴级函数有 histplot()、kdeplot()、ecdfplot() 和 rugplot()。它们在图形级 displot()、jointplot() 和 pairplot() 函数中进行分组。

有几种不同的方法来可视化分布，每种方法都有其相对优势和劣势。了解这些因素很重要，以便您可以为您的特定目标选择最佳方法。

绘制单变量直方图

也许可视化分布最常见的方法是直方图。这是 displot() 中的默认方法，它使用与 histplot() 相同的底层代码。直方图是一个条形图，其中表示数据变量的轴被划分为一组离散的 bin，并且落在每个 bin 中的观测值的数量使用相应条形的高度显示

penguins = sns.load_dataset("penguins")
sns.displot(penguins, x="flipper_length_mm")

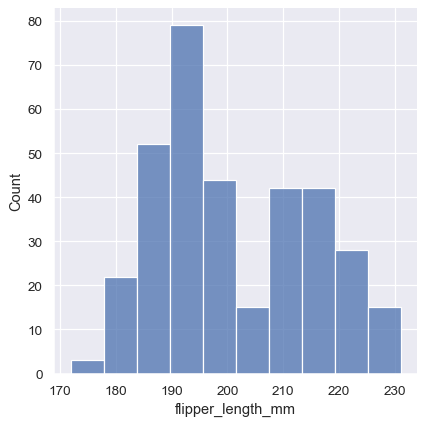
此图立即提供了关于 flipper_length_mm 变量的一些见解。例如，我们可以看到最常见的鳍长约为 195 毫米，但分布似乎是双峰的，因此这个数字不能很好地代表数据。

选择 bin 大小

bin 的大小是一个重要参数，使用错误的 bin 大小可能会通过隐藏数据的关键特征或通过从随机可变性中创建明显的特征而产生误导。默认情况下，displot()/histplot() 根据数据的方差和观测值的数量选择默认的 bin 大小。但是，您不应该过分依赖此类自动方法，因为它们取决于对数据结构的特定假设。始终建议检查您对分布的印象是否在不同的 bin 大小上保持一致。要直接选择大小，请设置 binwidth 参数

sns.displot(penguins, x="flipper_length_mm", binwidth=3)

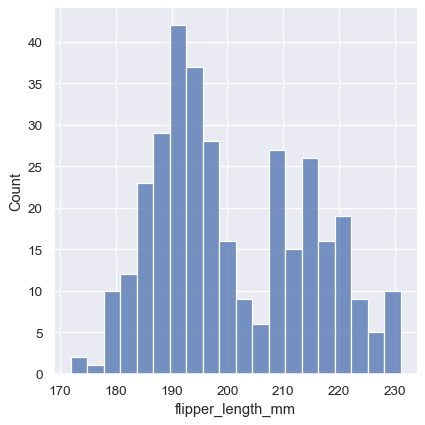
在其他情况下，指定数量的 bin 而不是它们的大小可能更有意义

sns.displot(penguins, x="flipper_length_mm", bins=20)

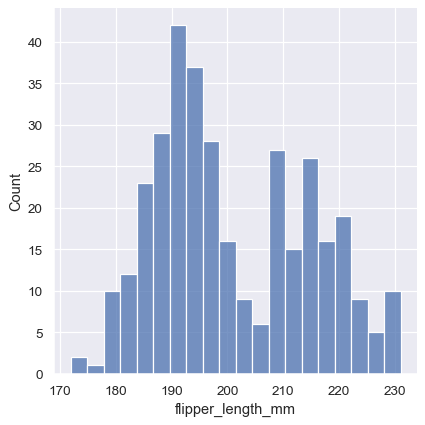
默认值失败的一种情况示例是当变量取相对较少的整数值时。在这种情况下，默认的 bin 宽度可能太小，在分布中创建尴尬的间隙

tips = sns.load_dataset("tips")
sns.displot(tips, x="size")

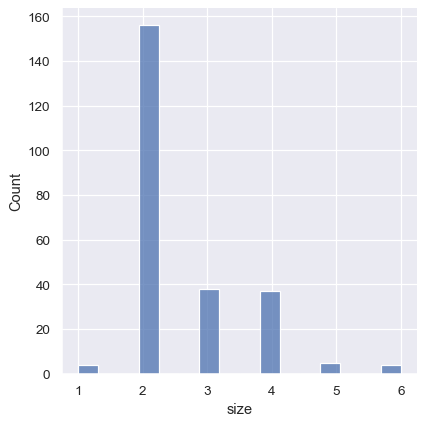
一种方法是通过将数组传递给 bins 来指定精确的 bin 分隔符

sns.displot(tips, x="size", bins=[1, 2, 3, 4, 5, 6, 7])

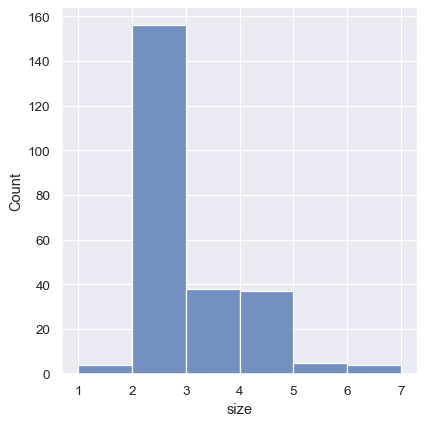
这也可以通过设置 discrete=True 来实现，它选择表示具有以对应值居中的条形的具有唯一值的集合中的 bin 分隔符。

sns.displot(tips, x="size", discrete=True)

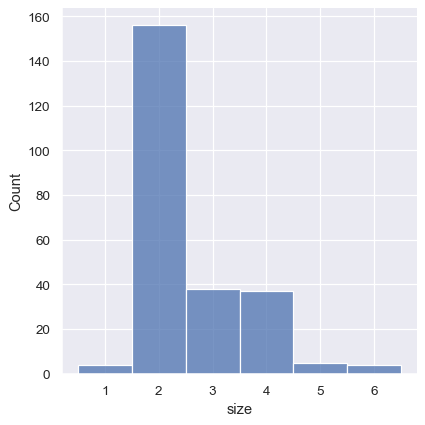
也可以使用直方图的逻辑来可视化分类变量的分布。分类变量会自动设置离散 bin，但略微“缩小”条形可能也有助于强调轴的分类性质

sns.displot(tips, x="day", shrink=.8)

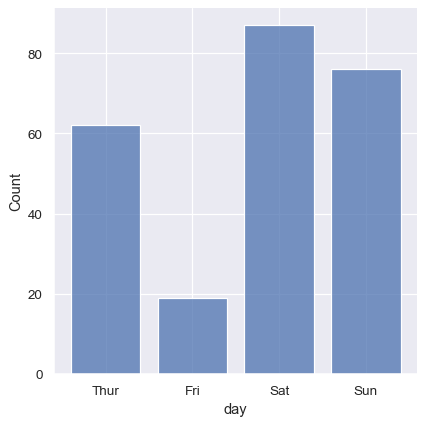
根据其他变量进行条件化

一旦您了解了变量的分布，下一步通常是询问该分布的特征是否因数据集中的其他变量而异。例如，是什么导致了我们上面看到的鳍长的双峰分布？displot() 和 histplot() 通过 hue 语义提供对条件子集的支持。将变量分配给 hue 将为其每个唯一值绘制一个单独的直方图，并通过颜色区分它们

sns.displot(penguins, x="flipper_length_mm", hue="species")

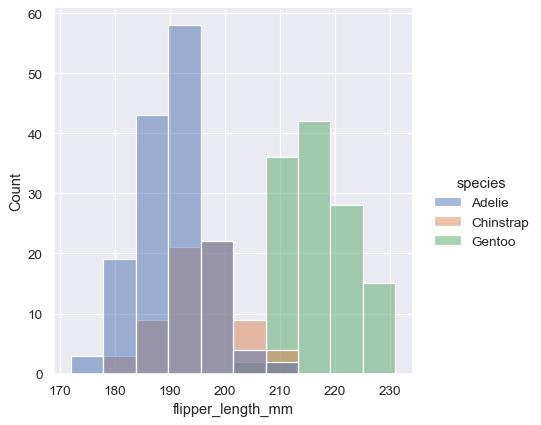
默认情况下，不同的直方图“叠加”在彼此之上，在某些情况下，它们可能很难区分。一种选择是将直方图的视觉表示从条形图更改为“步骤”图

sns.displot(penguins, x="flipper_length_mm", hue="species", element="step")

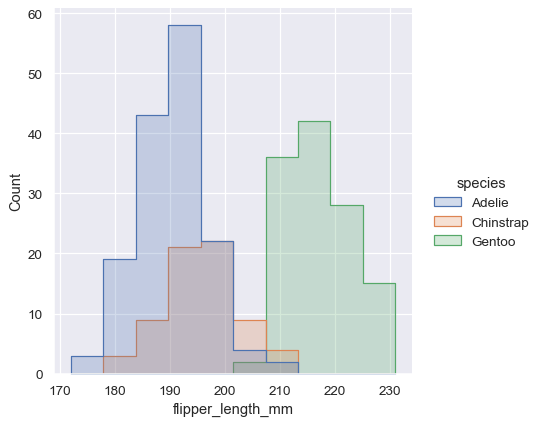
或者，可以“堆叠”每个条形，而不是叠加它们，或者垂直移动它们。在此图中，完整直方图的轮廓将与只有一个变量的图匹配

sns.displot(penguins, x="flipper_length_mm", hue="species", multiple="stack")

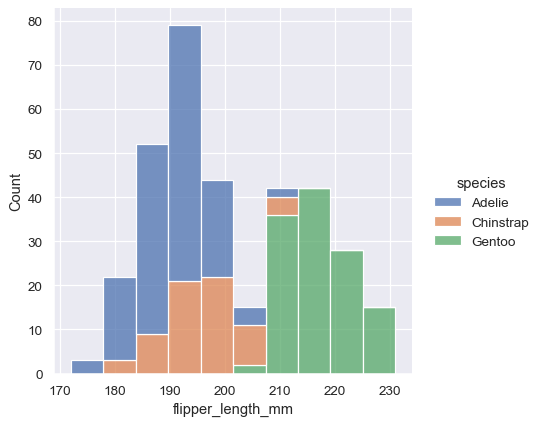
堆叠直方图强调了变量之间的部分-整体关系，但它可能会掩盖其他特征（例如，很难确定 Adelie 分布的众数。另一种选择是“躲避”条形，这会将它们水平移动并减小它们的宽度。这确保了没有重叠，并且条形在高度方面保持可比性。但这仅在分类变量的级别很少时才有效

sns.displot(penguins, x="flipper_length_mm", hue="sex", multiple="dodge")

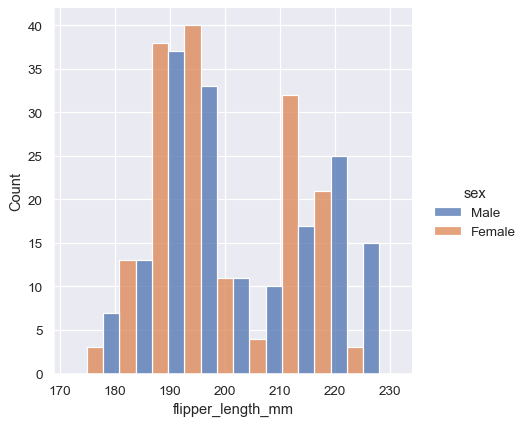
由于 displot() 是一个图形级函数，并且绘制在 FacetGrid 上，因此也可以通过将第二个变量分配给 col 或 row 而不是（或除）hue 来在单独的子图中绘制每个单独的分布。这很好地表示了每个子集的分布，但它使得直接比较更加困难

sns.displot(penguins, x="flipper_length_mm", col="sex")

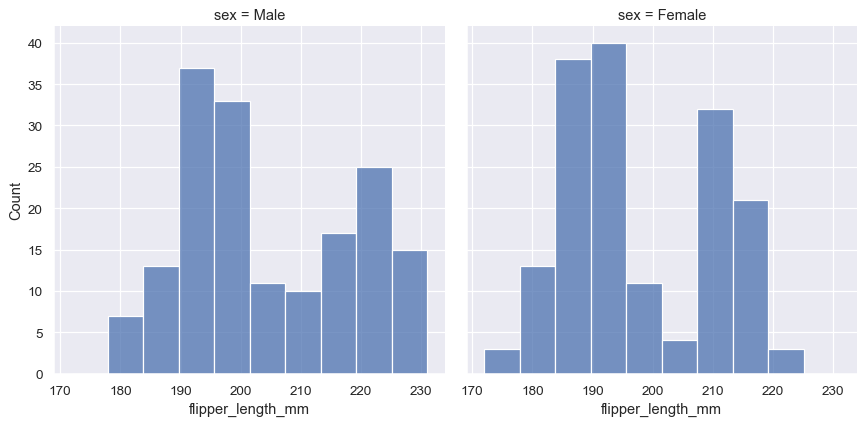
这些方法都不是完美的，我们很快就会看到一些更适合比较任务的直方图替代方案。

归一化直方图统计

在我们这样做之前，需要注意的另一点是，当子集具有不平等的观测值数量时，根据计数比较它们的分布可能不理想。一种解决方案是使用 stat 参数归一化计数

sns.displot(penguins, x="flipper_length_mm", hue="species", stat="density")

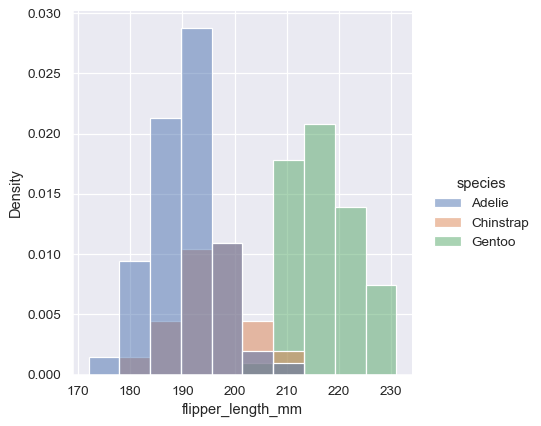
但是，默认情况下，归一化应用于整个分布，因此这只是重新缩放条形的高度。通过设置 common_norm=False，每个子集将独立归一化

sns.displot(penguins, x="flipper_length_mm", hue="species", stat="density", common_norm=False)

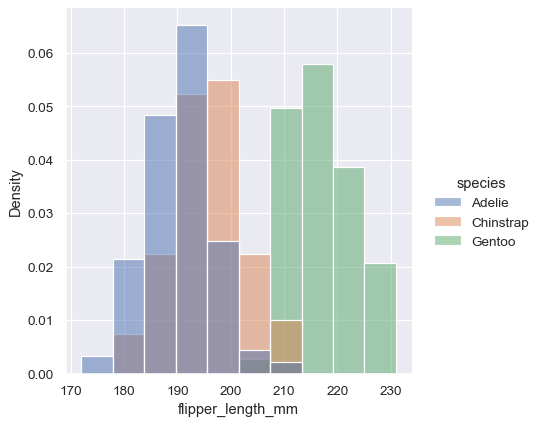
密度归一化缩放条形，使它们的面积之和为 1。因此，密度轴不能直接解释。另一种选择是将条形归一化为其高度之和为 1。当变量是离散的时，这最有意义，但它是所有直方图的一个选项

sns.displot(penguins, x="flipper_length_mm", hue="species", stat="probability")

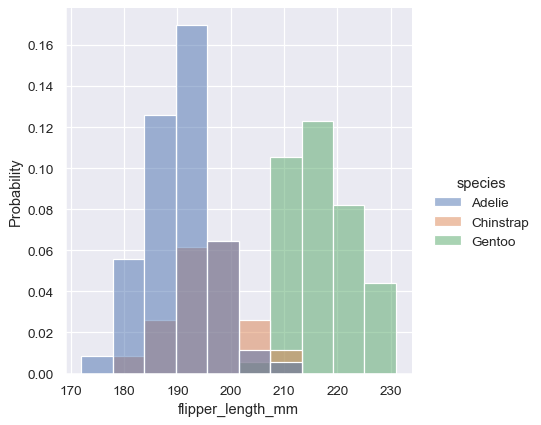
核密度估计

直方图旨在通过将观测值分组到 bin 并计数来近似生成数据的潜在概率密度函数。核密度估计 (KDE) 为同一个问题提供了不同的解决方案。KDE 图不是使用离散 bin，而是用高斯核平滑观测值，产生连续的密度估计

sns.displot(penguins, x="flipper_length_mm", kind="kde")

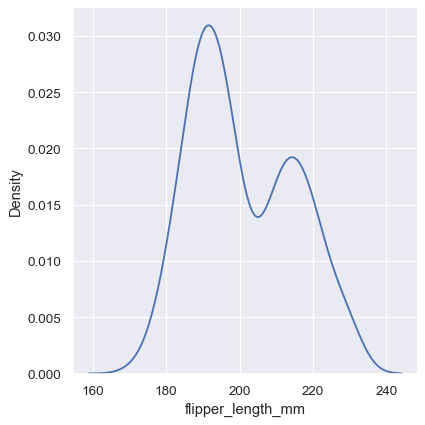
选择平滑带宽

与直方图中的 bin 大小非常相似，KDE 准确表示数据的 ability 取决于平滑带宽的选择。过度平滑的估计可能会抹去有意义的特征，但过度平滑的估计可能会将真正的形状隐藏在随机噪声中。检查估计稳健性的最简单方法是调整默认带宽

sns.displot(penguins, x="flipper_length_mm", kind="kde", bw_adjust=.25)

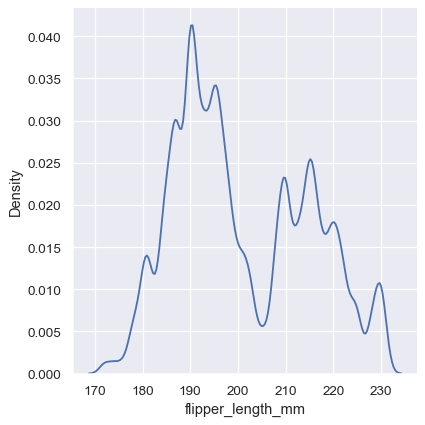
请注意，窄带宽使双峰性更加明显，但曲线光滑得多。相反，较大的带宽几乎完全掩盖了双峰性

sns.displot(penguins, x="flipper_length_mm", kind="kde", bw_adjust=2)

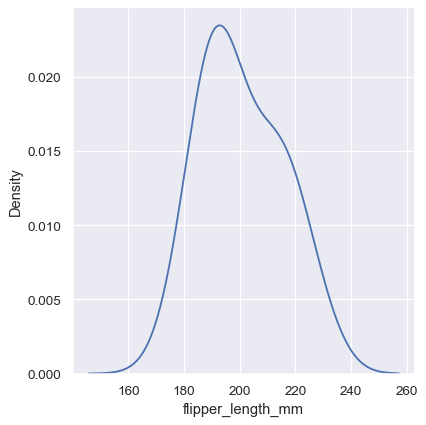
根据其他变量进行条件化

与直方图一样，如果您分配了一个 hue 变量，则会为该变量的每个级别计算一个单独的密度估计

sns.displot(penguins, x="flipper_length_mm", hue="species", kind="kde")

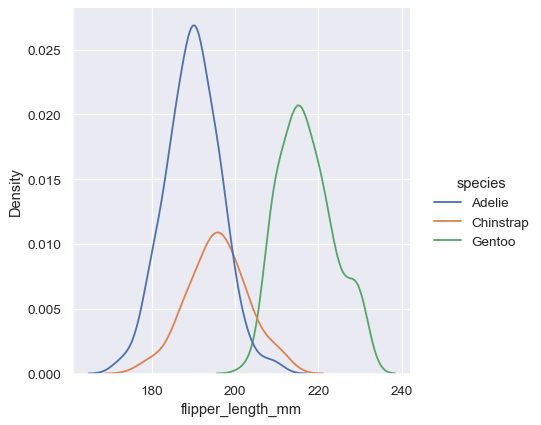
在许多情况下，叠加的 KDE 比叠加的直方图更容易解释，因此它通常是比较任务的不错选择。但是，许多相同的分辨多个分布的选项也适用于 KDE

sns.displot(penguins, x="flipper_length_mm", hue="species", kind="kde", multiple="stack")

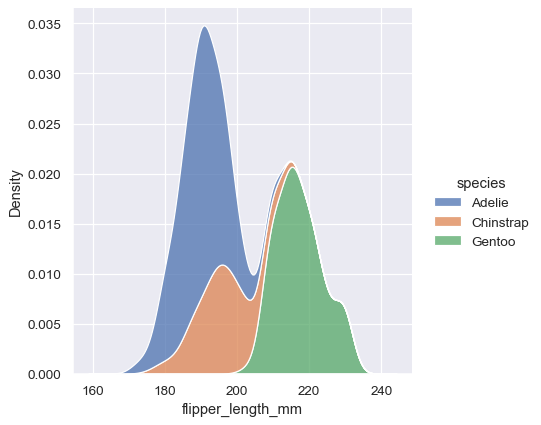
请注意，堆叠图默认情况下会填充每条曲线之间的区域。也可以填充单层或多层密度的曲线，尽管默认的 alpha 值（不透明度）会有所不同，以便更容易分辨各个密度。

sns.displot(penguins, x="flipper_length_mm", hue="species", kind="kde", fill=True)

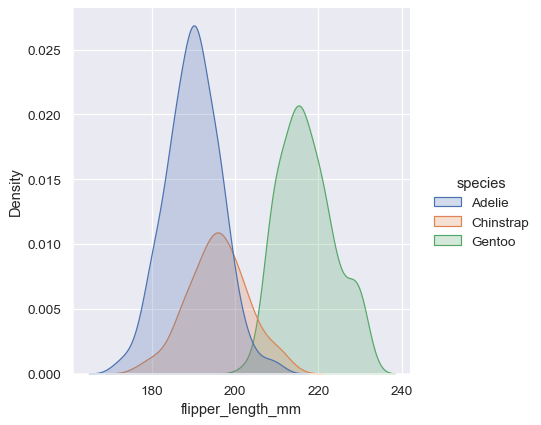
核密度估计的缺陷

KDE 图有很多优点。数据的重要特征很容易辨别（集中趋势、双峰性、偏度），并且可以轻松比较子集。但也有 KDE 无法很好地表示基础数据的情况。这是因为 KDE 的逻辑假设基础分布是平滑且无界的。这种假设失败的一种方式是当一个变量反映一个自然有界的量时。如果有一些观测值位于边界附近（例如，一个不能为负的变量的小值），则 KDE 曲线可能会延伸到不切实际的值。

sns.displot(tips, x="total_bill", kind="kde")

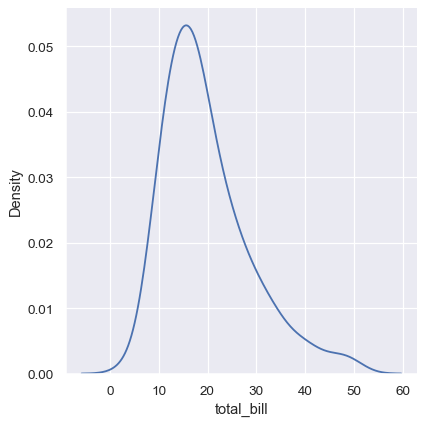
这可以通过 cut 参数来部分避免，该参数指定曲线应该延伸到极端数据点之外多远。但这只影响曲线绘制的位置；密度估计仍然会在没有数据存在的范围内进行平滑，导致它在分布的极端值处被人为地降低。

sns.displot(tips, x="total_bill", kind="kde", cut=0)

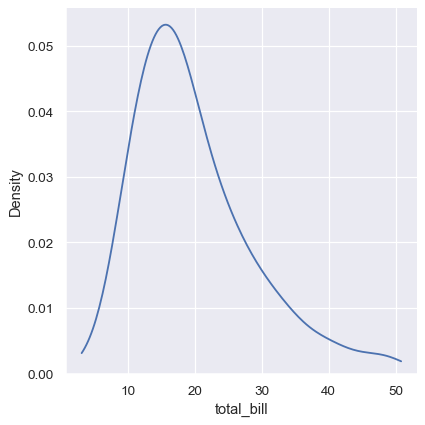
KDE 方法对于离散数据或数据自然连续但特定值被过度表示的情况也不起作用。需要记住的是，KDE 始终会显示一条平滑曲线，即使数据本身并不平滑。例如，请考虑这种钻石重量分布。

diamonds = sns.load_dataset("diamonds")
sns.displot(diamonds, x="carat", kind="kde")

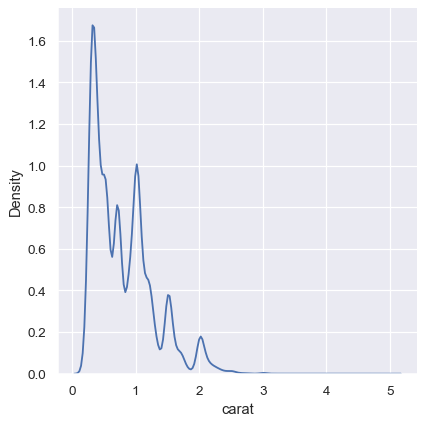
虽然 KDE 表明在特定值附近有峰值，但直方图显示了一个更加参差不齐的分布。

sns.displot(diamonds, x="carat")

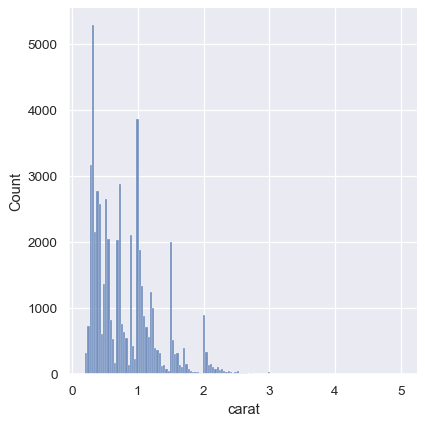
作为折衷方案，可以将这两种方法结合起来。在直方图模式下，displot()（与 histplot() 一样）可以选择包含平滑的 KDE 曲线（注意 kde=True，而不是 kind="kde"）。

sns.displot(diamonds, x="carat", kde=True)

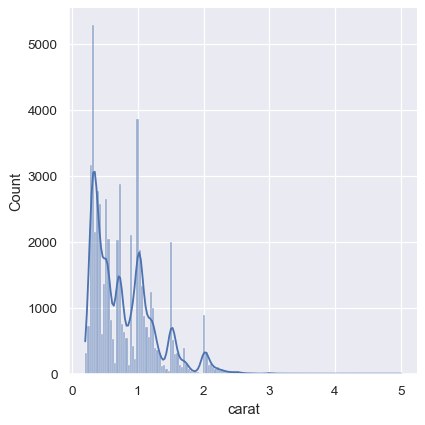
经验累积分布

可视化分布的第三个选项是计算“经验累积分布函数”（ECDF）。此图绘制了一条单调递增的曲线，穿过每个数据点，曲线的高度反映了具有较小值的观测值的比例。

sns.displot(penguins, x="flipper_length_mm", kind="ecdf")

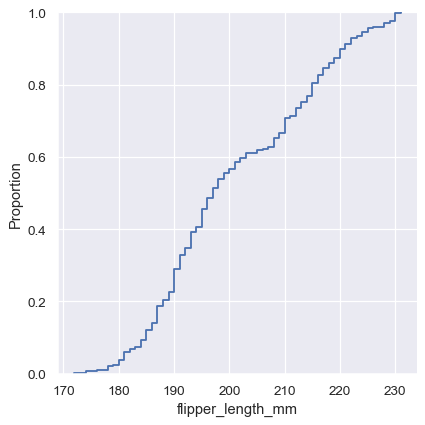
ECDF 图有两个主要优点。与直方图或 KDE 不同，它直接表示每个数据点。这意味着没有 bin 大小或平滑参数需要考虑。此外，由于曲线是单调递增的，因此它非常适合比较多个分布。

sns.displot(penguins, x="flipper_length_mm", hue="species", kind="ecdf")

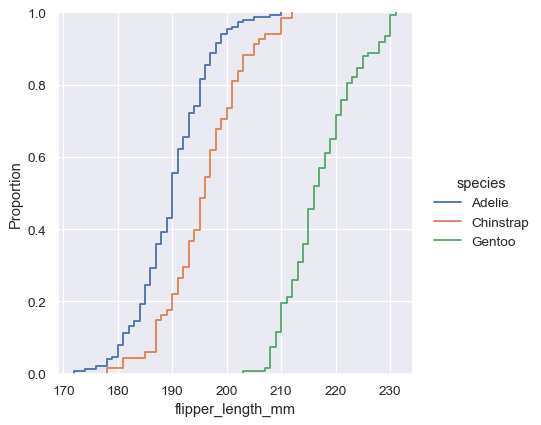
ECDF 图的主要缺点是，它比直方图或密度曲线更不直观地表示分布的形状。请考虑如何立即在直方图中清楚地看到鳍状肢长度的双峰性，但在 ECDF 图中，您必须寻找不同的斜率才能看到它。尽管如此，通过练习，您可以学会通过检查 ECDF 来回答有关分布的所有重要问题，并且这样做可能是一种有效的方法。

可视化双变量分布

到目前为止，所有示例都考虑了单变量分布：单个变量的分布，可能取决于分配给 hue 的第二个变量。但是，将第二个变量分配给 y 将绘制一个双变量分布。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm")

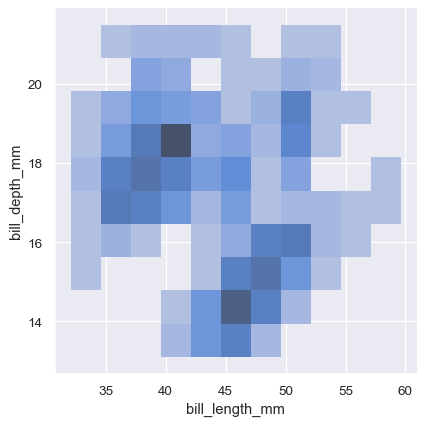
双变量直方图将数据放入平铺图的矩形中，然后用填充色（类似于 heatmap()）显示每个矩形中观测值的计数。类似地，双变量 KDE 图使用二维高斯函数对 (x, y) 观测值进行平滑。然后，默认表示显示了二维密度的轮廓。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", kind="kde")

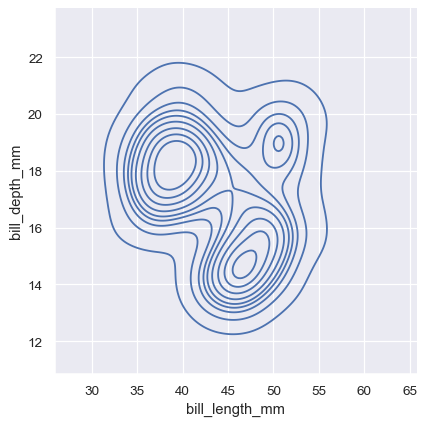
分配一个 hue 变量将使用不同的颜色绘制多个热图或轮廓集。对于双变量直方图，只有在条件分布之间几乎没有重叠时，此方法才能正常工作。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", hue="species")

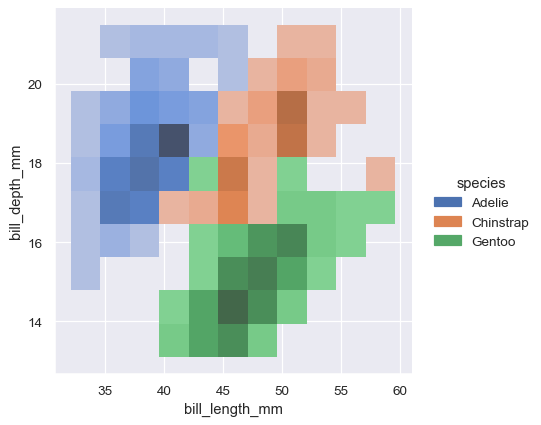
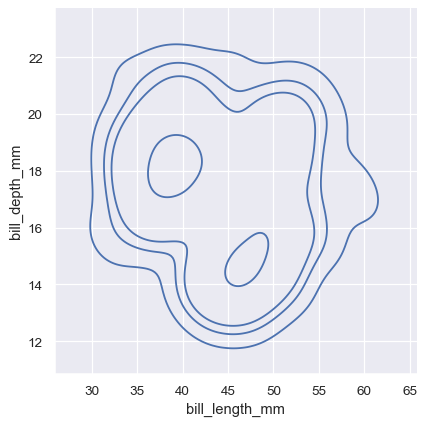
双变量 KDE 图的轮廓方法更适合于评估重叠，尽管轮廓过多的图可能会变得很乱。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", hue="species", kind="kde")

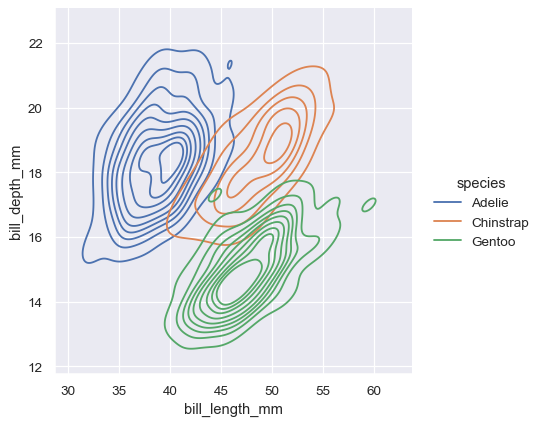
与单变量图一样，bin 大小或平滑带宽的选择将决定图对底层双变量分布的表示程度。相同的参数适用，但可以通过传递一对值来针对每个变量进行调整。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", binwidth=(2, .5))

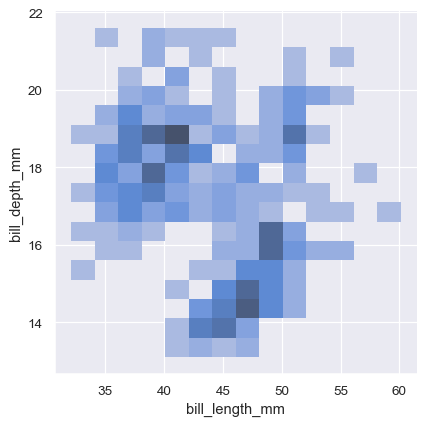
为了帮助解释热图，请添加一个颜色条以显示计数和颜色强度之间的映射。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", binwidth=(2, .5), cbar=True)

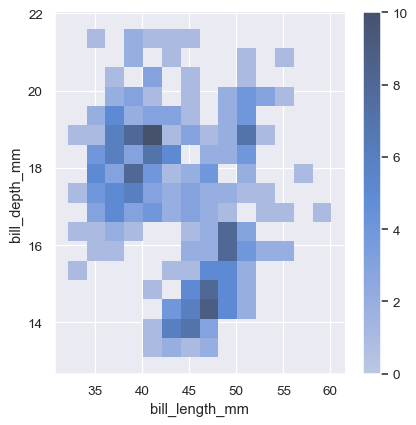
双变量密度轮廓的含义不太直观。因为密度本身无法直接解释，所以轮廓是在密度的等比例处绘制的，这意味着每条曲线都显示了一个水平集，使得密度的某个比例 p 位于其下方。p 值是均匀间隔的，最低级别由 thresh 参数控制，数量由 levels 控制。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", kind="kde", thresh=.2, levels=4)

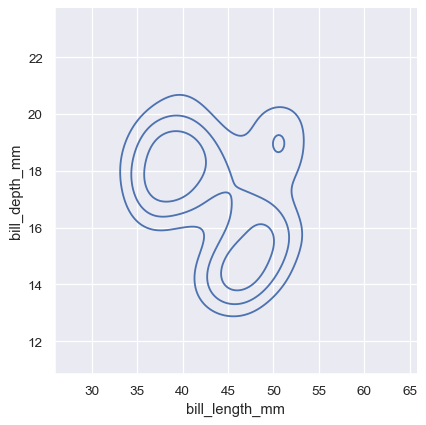
为了更好地控制，levels 参数也接受一个值列表。

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", kind="kde", levels=[.01, .05, .1, .8])

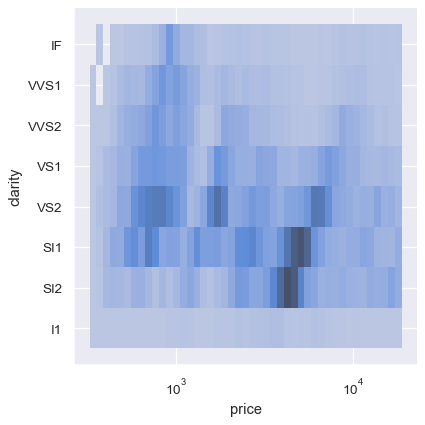
双变量直方图允许一个或两个变量是离散的。绘制一个离散变量和一个连续变量提供了另一种比较条件单变量分布的方法。

sns.displot(diamonds, x="price", y="clarity", log_scale=(True, False))

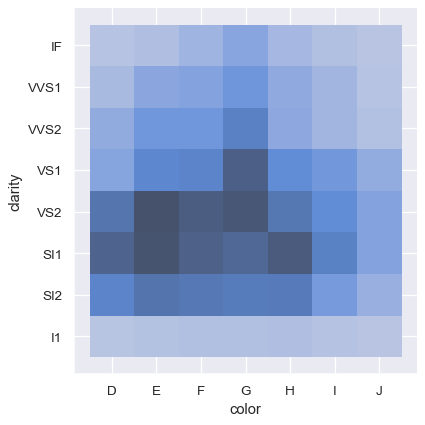
相比之下，绘制两个离散变量是一种简单的方法，可以显示观测值的交叉表。

sns.displot(diamonds, x="color", y="clarity")

其他设置中的分布可视化

Seaborn 中的几个其他图级绘图函数使用了 histplot() 和 kdeplot() 函数。

绘制联合和边缘分布

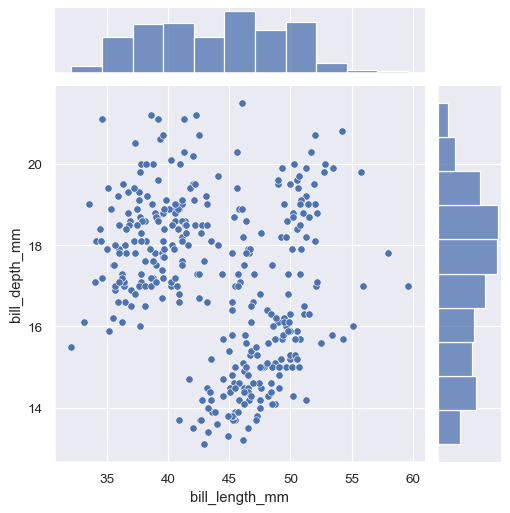
第一个是 jointplot()，它通过两个变量的边缘分布来增强双变量关系或分布图。默认情况下，jointplot() 使用 scatterplot() 表示双变量分布，使用 histplot() 表示边缘分布。

sns.jointplot(data=penguins, x="bill_length_mm", y="bill_depth_mm")

与 displot() 类似，在 jointplot() 中设置不同的 kind="kde" 将更改联合图和边缘图，使其使用 kdeplot()。

sns.jointplot(
    data=penguins,
    x="bill_length_mm", y="bill_depth_mm", hue="species",
    kind="kde"
)

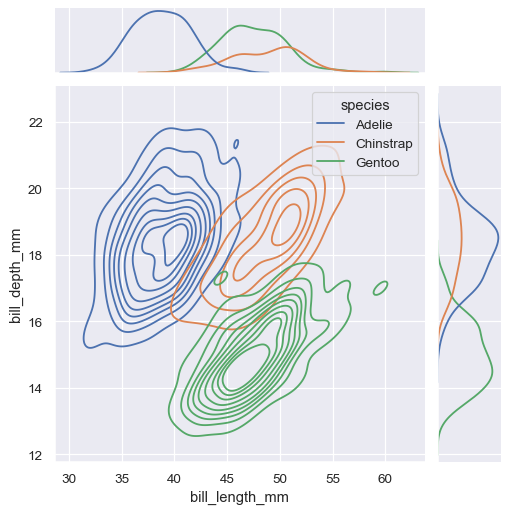
jointplot() 是 JointGrid 类的便捷接口，该接口在直接使用时提供了更多灵活性。

g = sns.JointGrid(data=penguins, x="bill_length_mm", y="bill_depth_mm")
g.plot_joint(sns.histplot)
g.plot_marginals(sns.boxplot)

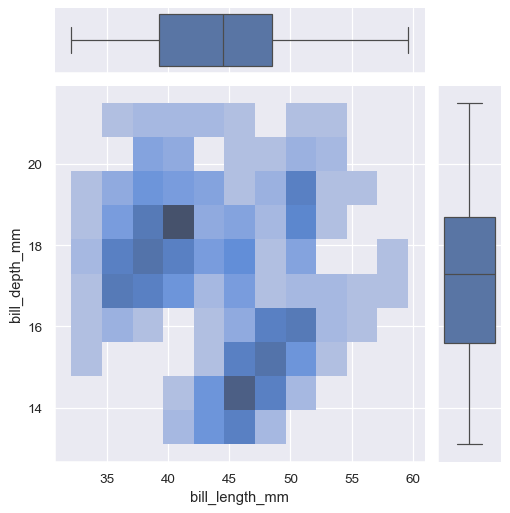
一种不太显眼的方式来显示边缘分布是使用“毛毯”图，它在图的边缘添加一个小的刻度以表示每个单独的观测值。这内置在 displot() 中。

sns.displot(
    penguins, x="bill_length_mm", y="bill_depth_mm",
    kind="kde", rug=True
)

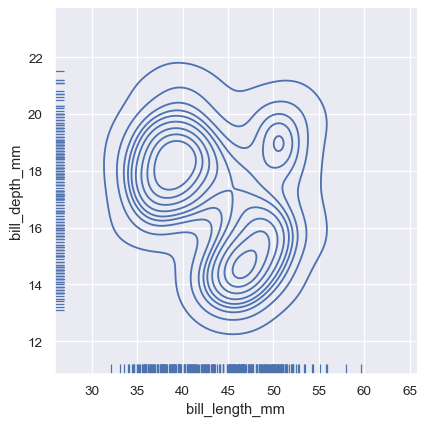
轴级 rugplot() 函数可用于在任何其他类型图的侧面添加毛毯。

sns.relplot(data=penguins, x="bill_length_mm", y="bill_depth_mm")
sns.rugplot(data=penguins, x="bill_length_mm", y="bill_depth_mm")

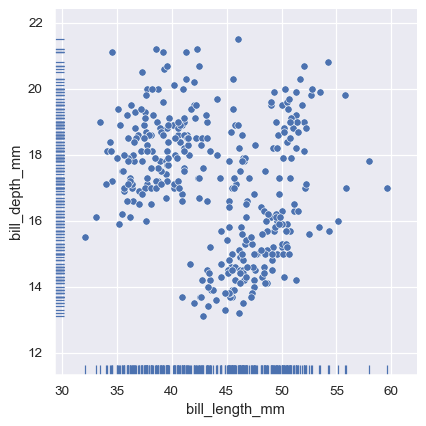
绘制多个分布

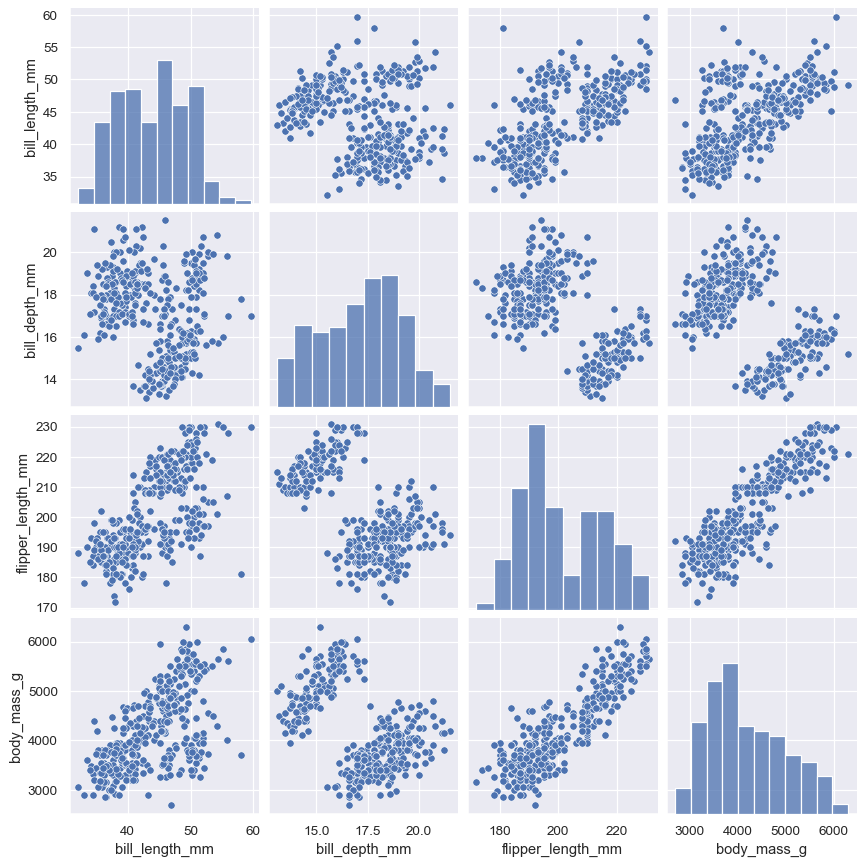
函数 pairplot() 提供了类似的联合和边缘分布混合。然而，与 jointplot() 相比，pairplot() 使用“小型多重”方法来可视化数据集中所有变量的单变量分布以及它们的所有成对关系。

sns.pairplot(penguins)

与 jointplot() / JointGrid 一样，使用底层的 PairGrid 可以提供更多灵活性，只需多输入一些内容。

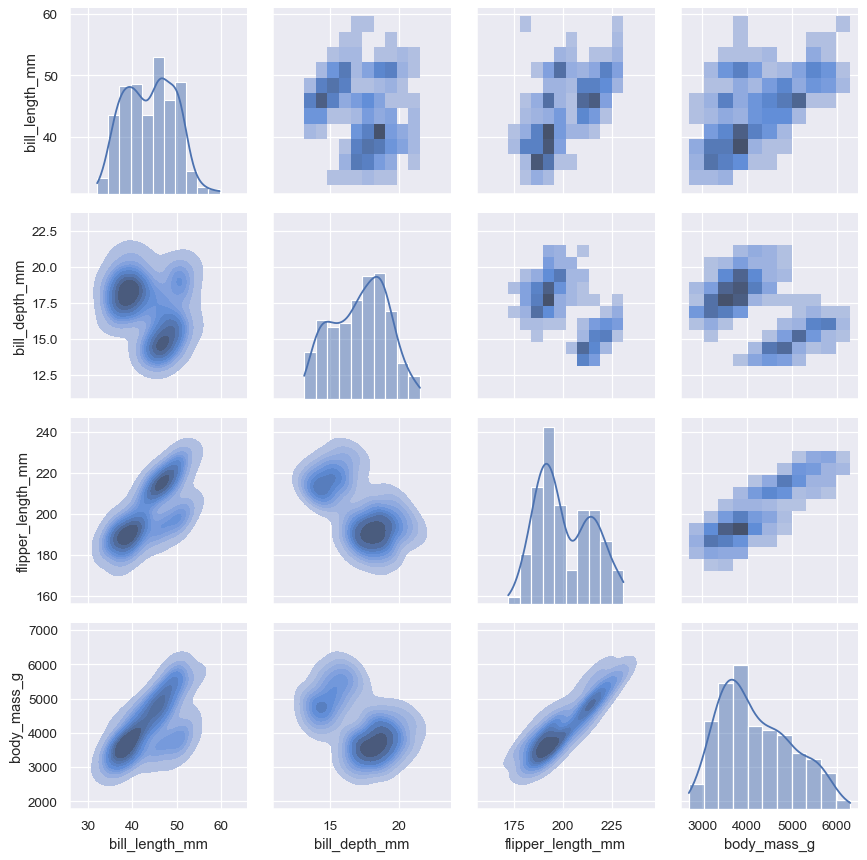
g = sns.PairGrid(penguins)
g.map_upper(sns.histplot)
g.map_lower(sns.kdeplot, fill=True)
g.map_diag(sns.histplot, kde=True)